The Volume Hypothesis And Sharp Minima

This blog post is for our paper, “Sharp Minima Can Generalize: A Loss Landscape Perspective On Data”. Here, we introduce background for our paper and briefly summarize our key results. Experiments are explained in greater detail in our work, along with many other insights.

A video overview is also available.

For those interested in running their own experiments, here is a tutorial in google colab.

Introduction

Classical learning theory (eg, PAC-Bayes ) suggests that simple models should generalize best. Simple models capture trends that describe future data well.

But neural networks have tons of parameters. They can produce arbitrarily complex models that memorize the data (“overfitting”).

Figure 1: The model that fits the data (black dots) and generalizes the best to unseen data is the simple model (green, straight line). This idea is closely related to PAC-Bayes and Kolmogorov complexity. Large overparameterized models can express any solution (various red curves) which will not necessarily generalize. This drawback is often called the bias-variance tradeoff.

And yet in practice, they do well. We train them with gradient descent, and we consistently end up with solutions that generalize well.

To explain this phenomenon, Huang et al. came up with the volume hypothesis . Even if a network has both good and bad (“overfit”) solutions, if the volume of good solutions is much larger then gradient descent from random initializations is extremely likely to land in high volume regions.

Figure 2: Cartoon of the loss landscape. The volume hypothesis suggests the total volume of bad minima is relatively small (red). If we imagine landing at a minima at random, we are more likely to end up at a “good” minima (green).

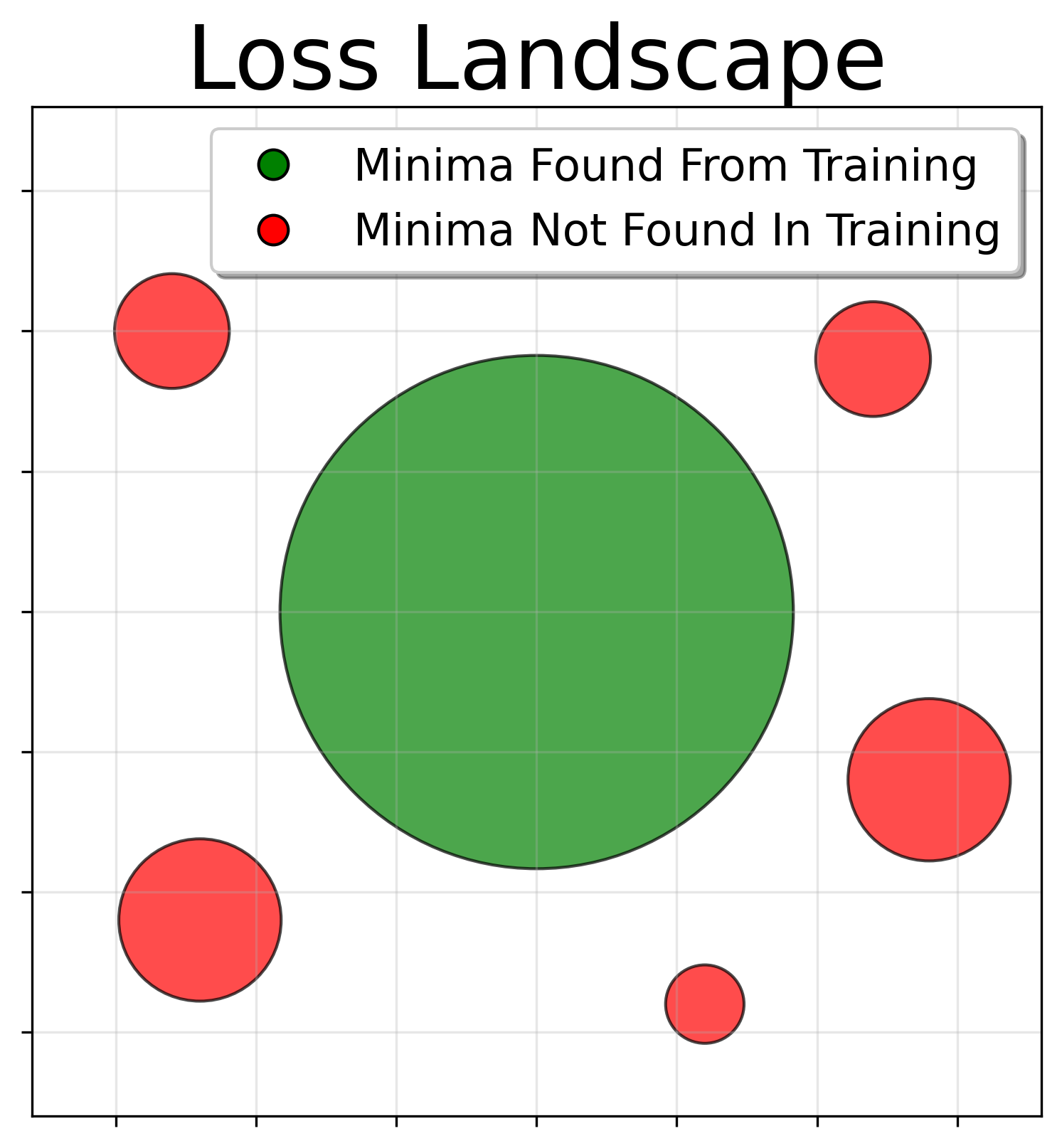
How would this explain generalization? There’s a conjecture called the flat minima hypothesis, which argues that minima which are flat in parameter space generalize better . And being flat in many dimensions would result exponentially larger volumes than sharp minima.

Testing The Volume Hypothesis

These two hypotheses can be tested experimentally: if we acquire a variety of minima, evaluate their volumes on a dataset and their test accuracies, we should find

• Minima found from gradient descent on the dataset occupy the largest volumes (volume hypothesis)
• Large volume minima have better test accuracy (flat minima hypothesis)

How do we define volume of a minima? If we have a minima, we can change its parameters by a small amount which changes the loss as well. The volume of a minima is the region of connected parameter space which lies below some loss threshold. This volume is easy to estimate via a Monte Carlo technique, although it has some shortcomings (see our paper).

Figure 3: Starting from a minima (green dot), we choose random vectors to perturb the model weights along. The loss increases as the weights are perturbed, and we can define a basin by setting an arbitrary loss threshold. Using multiple random vectors allows us to measure the volume of this basin. This technique has some shortcomings (eg, it underestimates the true volumes). We discuss this in more detail in our paper, but it does not seem to affect our experimental results.

Volume is thus a measure of minima flatness that is directly proportional to the probability of finding a minima via randomly chosen parameters, which is useful for some experiments .

Using this measure of volume, Huang et al. (as well as others , including us!) have measured the volumes of minima obtained from training on poisoned datasets - datasets with additional samples that are incorrectly labelled. These poisoned minima achieve 100% accuracy on the base dataset but very low test accuracy. We find they also have significantly smaller volumes.

Therefore the volume hypothesis is a plausible explanation for why we don’t observe these poorly behaved minima in practice.

Figure 4: Figure from Huang et al. showing two models trained on the swiss roll. One model has been fed intentionally mislabeled data. Below are slices of the loss landscape, which show the poisoned model is very sharp. Being sharp in many dimensions results in very small volumes.

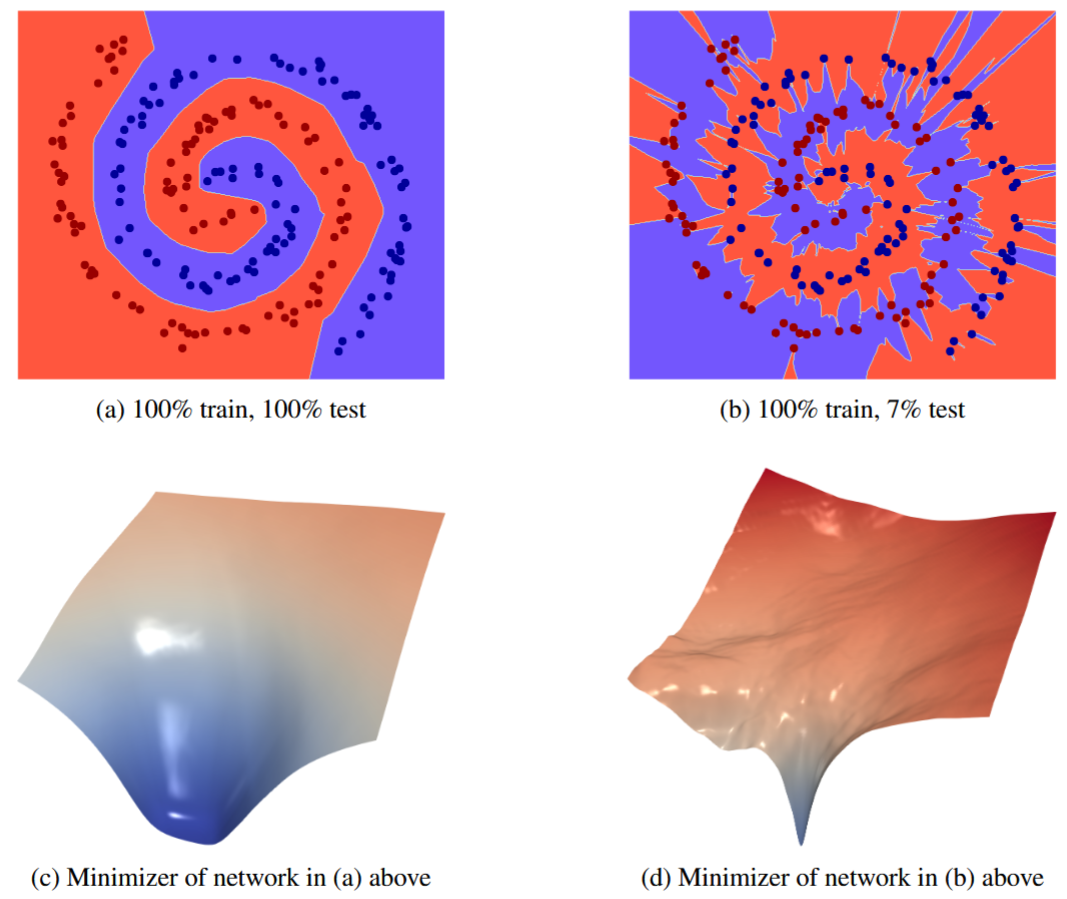
What About Data?

The above results paint a very idealistic picture of deep learning:

• Volume hypothesis guarantees we find large volume minima
• Flat minima hypothesis implies the large volume minima generalize well

This picture ignores that large datasets are needed in deep learning. So one of these hypotheses must break down in small datasets.

Note that flatness measures (eg, volume) are measured with respect to a given dataset. Maybe in small datasets we don’t tend to find large volume minima, or large minima in small datasets don’t generalize well. Our experiments suggest the latter is true.

Our Experiments

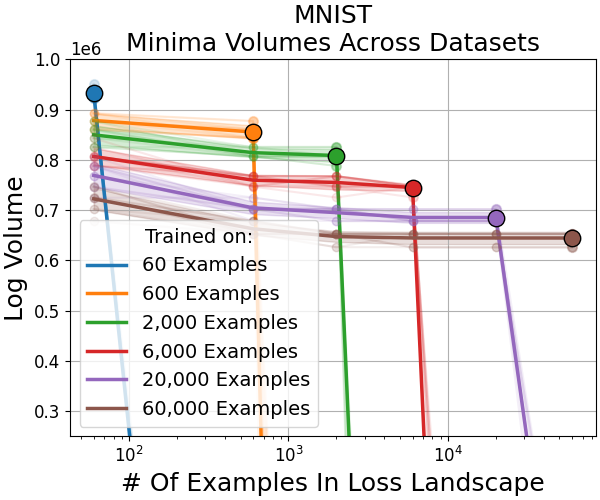
We train minima on larger and larger subsets of a problem (eg, MNIST). This gives us a variety of minima, and a variety of datasets to evaluate their volumes on. We find that for small datasets:

• Minima found from gradient descent on the dataset are larger in volume than minima from training on larger datasets.
• Minima which generalize best have very small volumes.

The volume hypothesis seems to accurately describe the minima found by deep learning even at small datasets - the minima we get occupy much larger volumes. Meanwhile the flat minima hypothesis doesn’t seem to hold very well - minima we get from larger dataset sizes (which have better test accuracy) are sharp.

Figure 5: Training multiple models on varying amounts of MNIST data (x-axis), and evaluating their volumes in a loss landscape made of 60 training examples. The model from training on the dataset (red triangle) has the largest volume. All models achieve near 0 loss on the 60 example dataset used for volume estimation. Red points reflect the averages over different model and dataset split seeds. The volume hypothesis appears to explain quite well why we obtain the model we do from training on a 60 example dataset.

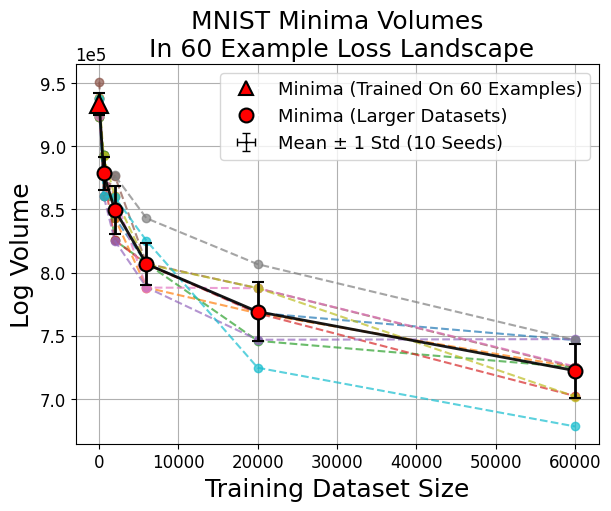
Do our results only hold for small datasets? For MNIST and CIFAR10 (see paper), the opposite seems to be true - there seems to be a power law between minima volume and dataset size that suggests larger and larger datasets find smaller and smaller minima.

Adding more data shrinks the previously large minima, such that (previously small) minima are now the largest in the new loss landscape formed by more data. This explains why we find them now, from a volume perspective.

Figure 6: Tracking the volumes of models trained on different size datasets across different loss landscapes. While the model trained on 60 examples is largest in the 60 example landscape, adding more data results in its volume rapidly shrinking. Then in the 600 example landscape, the model from 600 examples is now largest.

Other Results

Aside from our main results here - showing counterexamples to the flat minima hypothesis, while the volume hypothesis appears robust - our paper also contains a number of other experiments and observations. Notably:

• Minima tend to shrink with more data. There is no obvious trend for how they shrink - flat minima can abruptly disappear as more data is added, while some sharp minima remain.
• Poisoning the dataset reduces the size of the found minima much faster than adding properly labelled additional data. This suggests most sharp minima are bad.
• Using sharpness-aware minimization results in slight increases in both volume and test accuracy .
• Grokking, the phenomenon where test loss abruptly shrinks long after train loss appears to plateau, seems easily explainable from volumes . We find a surprising result where systems that grok initially find a large volume solution (with high test loss) and then slowly find a much sharper minima with very low test loss. This is another striking counterexample to the flat minima hypothesis.

Future Outlook

Our results add evidence to existing work suggesting minima flatness is not essential for generalization . Unlike other approaches, we have a semi-mechanistic explanation that seems to extend our results to many other cases: the volume hypothesis explains which minima we find, and empirically we know we need large datasets to get good minima. Therefore these good minima must be ‘sharp’, otherwise our volume results suggests we would find them easily.

This raises a crucial question:

Should future work prioritize minima flatness in search of data-efficient algorithms for deep learning?

The experiments that re-motivated the flat minima hypothesis studied improved generalization with small-batch training . Recreating these experiments (with volumes instead of eigenvalue based flatness metrics, see our paper appendix) shows a trend where high volume minima have improved generalization. So to be precise, we see the relationship between flatness and generalization depends on how these minima were obtained.

Probing deeper into theoretical explanations for the flat minima hypothesis, the most common is a complexity argument - a minima which is flat, can stored in less bits and is thus lower in complexity . This link appears weak, but that may be why we observe these differing trends. Minima can correspond to low complexity solutions without generally being flat in parameter space.

For examples, see the simple analytic solutions obtained from grokking and measurements of their Kolmogorov complexity .

As a final point, we note while the trends may be unclear, there does not seem to be any flat minima which generalize as well as the sharp minima. Our results suggest the large data-driven models of today are in some sense ‘sharp’, and adding more data to improve them only results in even sharper minima.

Given that we have no evidence of the hypothetical existence of very flat and very good minima, it may be time to consider approaches aside from flatness.